图卷积
图卷积网络Graph Convolutional Network,简称GCN。
$G=(V,E)$是图,图中有$N$个节点,每个节点有$F$维特征,输入图信号可以表示为$X \in N\times F$ 的矩阵。图的结构可以表示为邻接矩阵$A\in N \times N$ ,图的度矩阵为$D$是一个对角矩阵,对角线的元素等于邻接矩阵每一行的和。
拉普拉斯算子 $\Delta/\nabla^2$
拉普拉斯算子(Laplace Operator)是$n$维欧几里得空间中的一个二阶微分算子,定义为梯度$\nabla f$的散度$\nabla \cdot$。即$\Delta f = \nabla^2 f= \nabla \cdot \nabla f = div(gradf)$,假设f是n维函数,$\Delta f = \Sigma_i \frac{\partial^2 f}{\partial^2 x_i^2}$。

拉普拉斯算子推广到图上:

图拉普拉斯矩阵
普通的拉普拉斯矩阵
定义:$L = D - A$
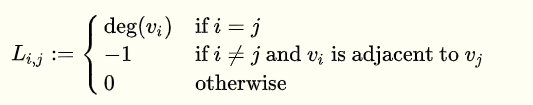
其中$deg(v_i)$表示节点i的度。

对称归一化的拉普拉斯 (Symmetric normalized Laplacian)
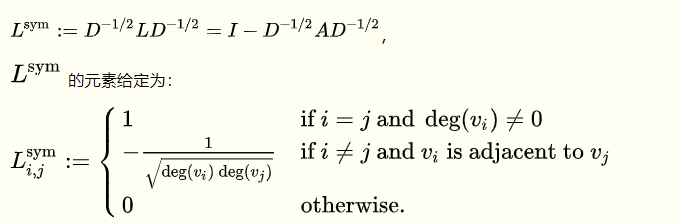
随机游走归一化的拉普拉斯 (Random walk normalized Laplacian)
??D-1*L还是D-1*A

泛化的拉普拉斯 (Generalized Laplacian)

拉普拉斯矩阵的半正定性
证明过程针对普通的拉普拉斯矩阵 $L=D-A$
- 拉普拉斯矩阵首先一定是一个实对称矩阵
- 拉普拉斯矩阵也是半正定矩阵

| 【首先证明L可以写出Incident Matrix矩阵的乘积,即$L=\nabla^T \nabla$,然后取非0向量$x$,证明$x^TLx \geq 0$恒成立即说明L是半正定矩阵(PSD)。$x^TLx = x^T \nabla^T \nabla x = (\nabla x)^T(\nabla x)$,$(\nabla x)$是一个向量,所以$x^TLx = | \nabla x | ^2$,由于$\nabla$矩阵的性质,每一行只有一个1,一个-1,其他全是0,所以结果等于$\Sigma(x_i-x_j)^2$,半正定得证。】 |
根据半正定性,有如下结论:
- L有n个非负的实数特征值(包括重根)。
- L有n个线性无关的实数特征向量。
- 存在由所有特征向量(需要进行归一化和正交化)构成的正交矩阵U,使得$U^TLU=\Lambda$(相似对角化),其中$\Lambda$是L的特征值构成的对角矩阵。
- 进一步可以推导出:$L=U\Lambda U^T$。
- $U=[u_1,u_2, …, u_n] \in R^{n \times n}$,任意的$u_i$都是$L$的特征向量,也就是满足$Lu_i = \lambda_i u_i$的值,其中$\lambda_i$为$L$的特征值。由于$L$是实对称矩阵,所以$U$是正交矩阵,满足$U^TU=UU^T=I$。
- $\Lambda$是特征值构成的对角矩阵:

图卷积
傅里叶变换
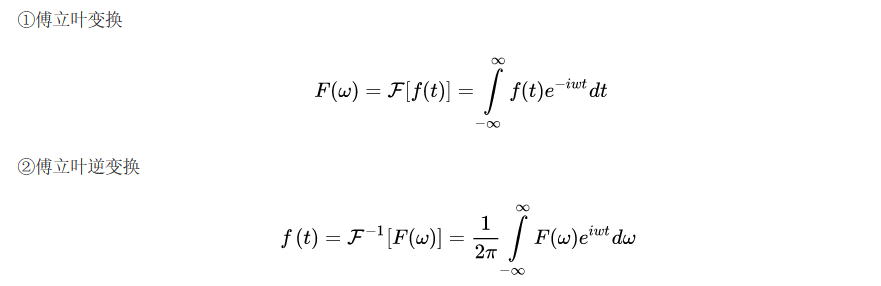
卷积定理

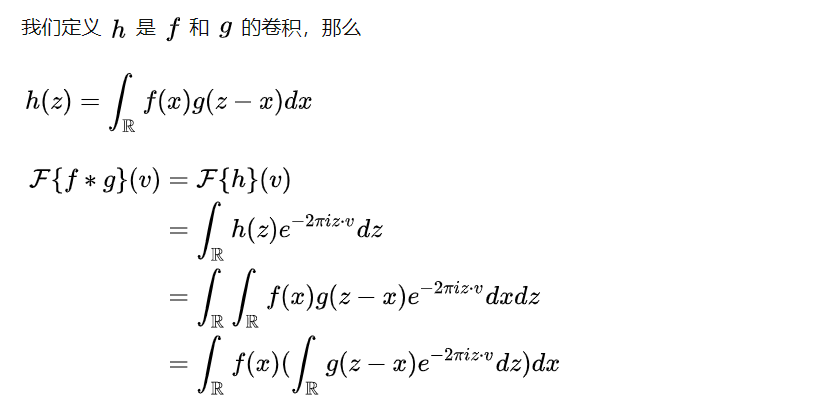
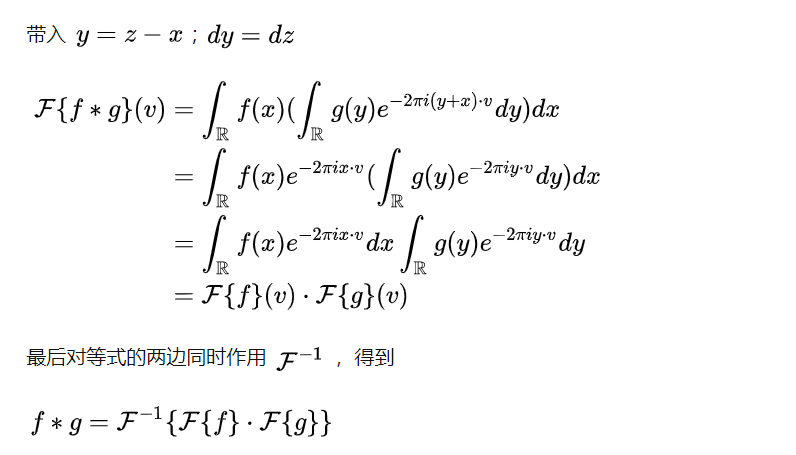
图的傅里叶变换/逆变换
$e^{-i\omega t}$称为傅里叶基 fouries basis,它是拉普拉斯算子的特征函数:
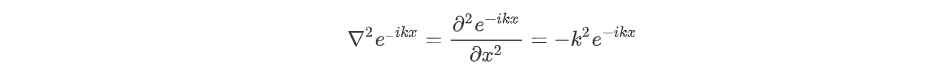
推广:
- 拉普拉斯算子对应于图的拉普拉斯矩阵$L$。
- 频率$\omega$对应于拉普拉斯矩阵的特征值$\lambda$。
- 傅里叶基$e^{-i\omega t}$对应于特征向量$u$。($U=[u_1,u_2, …, u_n] \in R^{n \times n}$)
图的傅里叶变换(傅里叶基是$U^T$)

即:

图的傅里叶逆变换(傅里叶基是$U$)

即:

图的卷积定理
原始的卷积定理:

推广:

作为图卷积的filter函数$g$,我们希望具有很好的局部性,可以把$g$定义成一个拉普拉斯矩阵的函数$g(L)$。
作用一次拉普拉斯矩阵相当于在图上传播了一次邻居节点。

所以得到图卷积公式:

$g_\theta(\Lambda)$的计算需要先计算拉普拉斯矩阵的特征值,比较复杂,使用Chebyshev多项式进行近似计算:


解释方法2:

取$K=1$,$\lambda{max} = 2$:
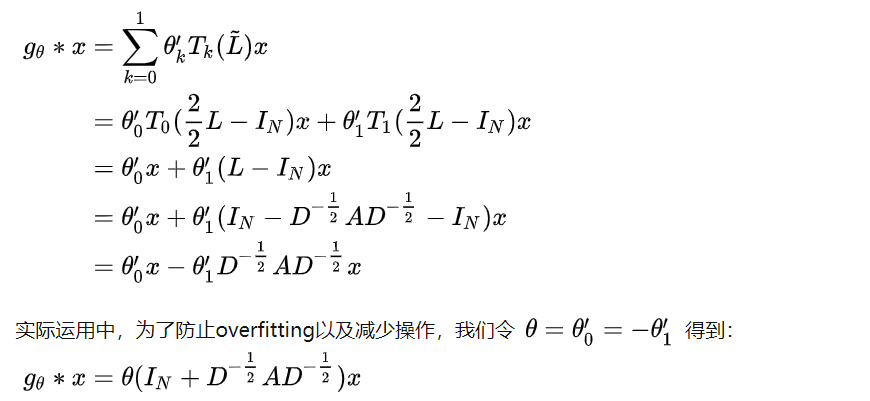
【下边这步不是完全相等的转换!】

图卷积
图卷积网络结构的定义:$H^{(l+1)} = f(H^{(l)}, A)$,
其中输入层$H^{(0)}=X \in N \times F$,输出层$H^{(L)}=Z \in N \times F$,$L$是层数。
不同的GCN模型采用不同的$f(\cdot,\cdot)$函数。
(1)层级传导
$f(H^{(l)}, A) = \sigma(AH^{(l)}W^{(l)})$,直接用$AH$矩阵相乘,然后通过权重矩阵$W^{(l)}$做线性变化,经过非线性激活函数$\sigma(\cdot)$,即可以得到当前层的输出,即下一层的输入$H^{(l+1)}$。
通过矩阵乘法,快速将相邻的节点的信息相加得到自己下一层的输入。
$A \in N \times N,H \in N \times F$,矩阵乘法就是A的每一行乘以H的每一列。A的第i行代表节点i的邻接点信息,相邻则为1,不相邻则为0;H的第j列代表这N个节点的第j个维度的特征。相乘求和,则与i不相邻的点的特征为0,相邻的点的特征被加到了一起,成为了输出矩阵中第i个点的第j维度的特征。
(2)矩阵添加自环
定义:$\tilde{A} = A + I$ ,因为在(1)的做法中,由于邻接矩阵A的对角线全0,矩阵AH相乘只考虑了周围节点,而为考虑自己本身,所以在A的基础上,补充对角线全1即可。
(3)矩阵归一化
由于矩阵相乘,会导致矩阵的值越来越大。所以可以对邻接矩阵进行归一化,使得其每一行的和为1,这样$AH$相乘得到的就是加权的结果,但是数值不会变得越来越大。
归一化方法1:每一行除以这一行的和即可。
$A=D^{-1}A$,即$A_{ij} = \frac{A_{ij}}{D_{ii}}$
归一化方法2:对称归一化。
$A=D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$,即$A_{ij} = \frac{A_{ij}}{\sqrt{d_i}\sqrt{d_j}}$
【这对应的就是不同的拉普拉斯矩阵】
(4)最后的结果
同时应用(2)和(3):
$f(H^{(l)}, A) = \sigma(\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})$,
其中$\hat{A}=A+I$,$\hat{D}$是$\hat{A}$的度矩阵,$\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}$则对$\hat{A}$进行了对称归一化。
参考
- https://zhuanlan.zhihu.com/p/107162772
- https://zhuanlan.zhihu.com/p/54505069
- https://zhuanlan.zhihu.com/p/124727955
- https://www.cnblogs.com/shiyublog/p/9785342.html
- http://www.huaxiaozhuan.com/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0/chapters/11_GNN.html
- https://davidham3.github.io/blog/2018/07/23/structured-sequence-modeling-with-graph-convolutional-recurrent-networks/
转载请标明如下内容:
本文作者:姜佳伟
本文链接:https://aptx1231.github.io/2021/02/14/%E5%9B%BE%E5%8D%B7%E7%A7%AF/
Github:aptx1231

