基础数学
行列式


向量内积 外积
内积/点积/数量积
【结果是一个数量】

外积/叉积/向量积
【结果是一个向量】

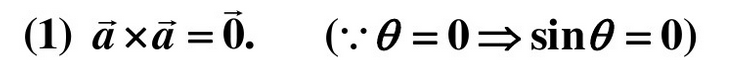
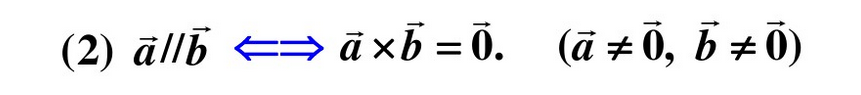
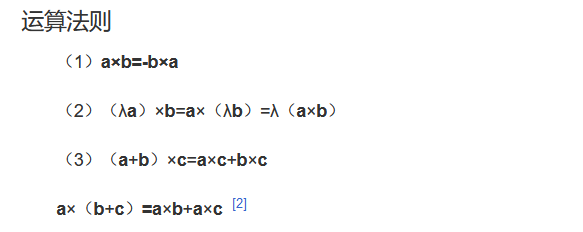
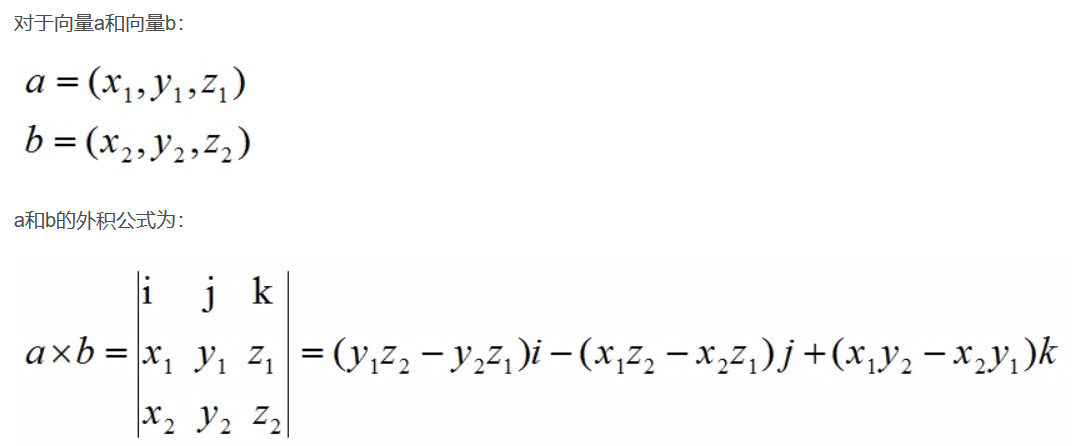
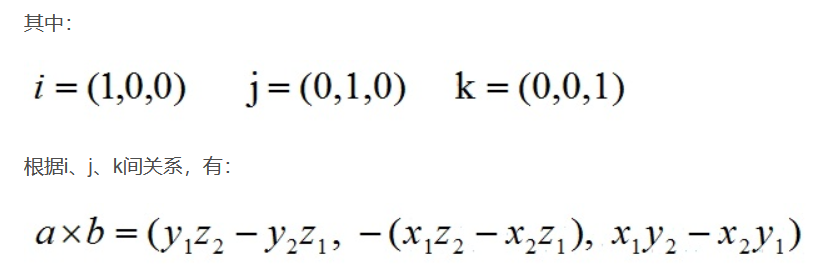
逆矩阵






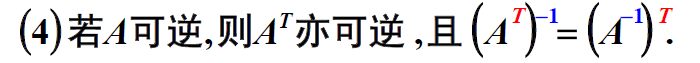
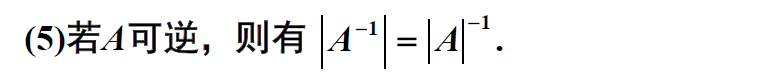
特征值 特征向量
定义






【n阶矩阵有n个特征值(算重根),因为n阶矩阵的特征多项式是n阶的】
性质








相似矩阵

‘

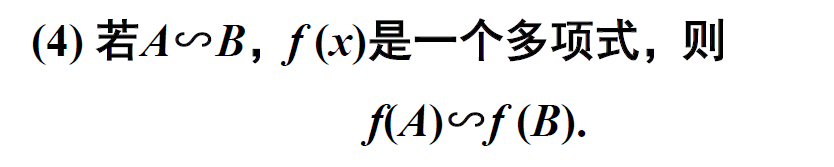


矩阵的相似对角化




步骤:
- 求特征值和特征向量
- 如果求出了n个线性无关的特征向量,那么由这n个向量组成的矩阵做Q,则A可以跟对角矩阵相似,且这个对角矩阵就是这n个特征向量对应的n个特征值(可以有重根)构成的对角矩阵
施密特正交化


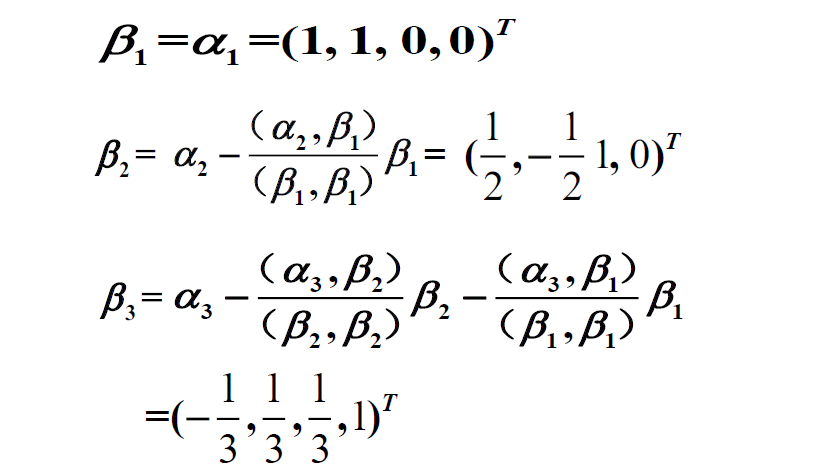
【最后还需要化成单位向量】
正交矩阵

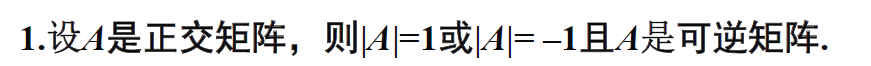
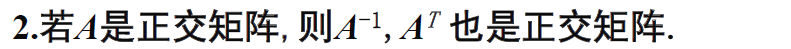
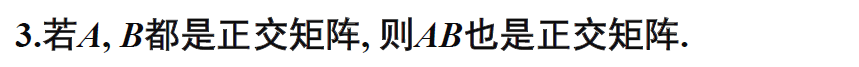

【行向量/列向量是两两正交的单位向量】
实对称矩阵
特征值与特征向量


相似对角化
实对称矩阵一定能相似对角化

步骤:
- 求特征值和特征向量
- 属于同一特征值的线性无关的特征向量要进行施密特正交化得到标准正交向量组
- 其他的特征向量也需要单位化
- 用所有的标准正交向量做列向量构成Q,则A可以跟对角矩阵相似,且这个对角矩阵就是这n个特征向量对应的n个特征值(可以有重根)构成的对角矩阵。【Q就是归一化之后的特征向量构成的矩阵】
合同矩阵



【A是对称矩阵,则B也是对称矩阵】
二次型
定义



可逆线性变换



【二次型进行可逆线性变换,相当于二次型对应的矩阵在进行合同变换,变换前后的矩阵合同】
标准二次型


实二次型
正交合同变换
对于实二次型,矩阵是实对称矩阵,而实对称矩阵都能相似对角化,所以



惯性定理






正定二次型




正定矩阵
只有实对称矩阵才考虑正定性
给定一个大小为 n×n 的实对称矩阵 A ,若对于任意长度为 n 的非零向量 X,有 \(X^TA X>0\) 恒成立,则矩阵 A 是一个正定矩阵(positive definite, PD)。
给定一个大小为 n×n 的实对称矩阵 A ,若对于任意长度为 n 的非零向量 X,有 \(X^TA X \geq 0\) 恒成立,则矩阵 A 是一个半正定矩阵(positive semi-definite, PSD)。
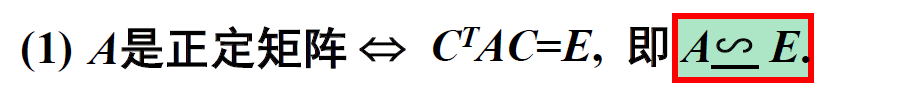
【因为A对应的正定二次型的规范型的矩阵是对角全1的对角矩阵,就是E】

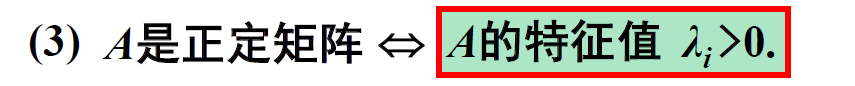
【因为A对应的正定二次型的标准型就是A的特征值做对角线的对角矩阵,且正定说明,对角线全大于0】



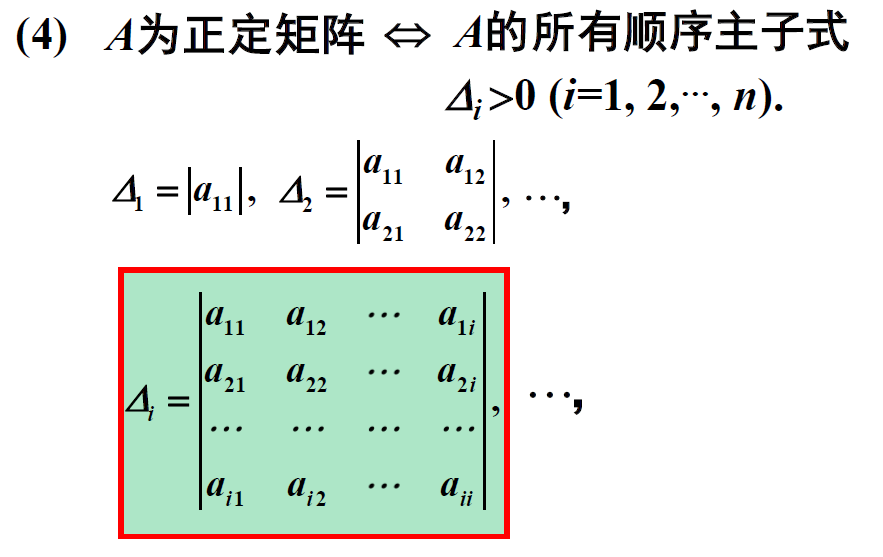


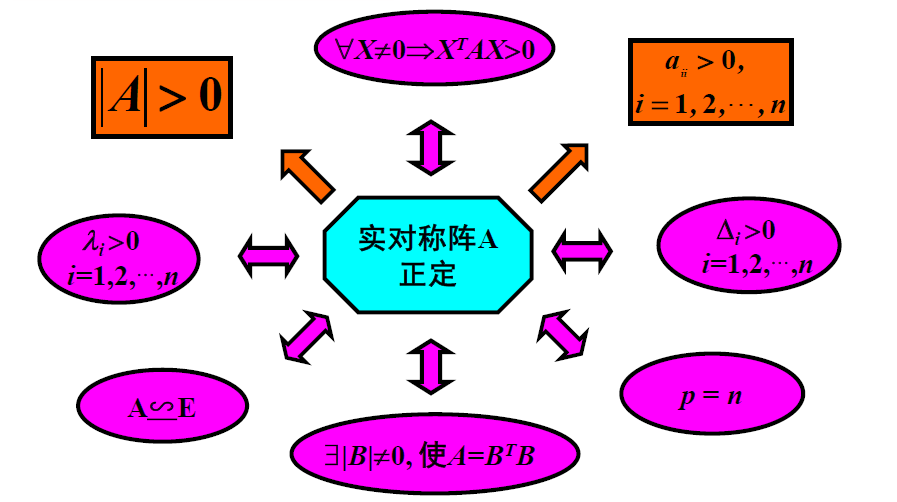



泰勒公式
微分


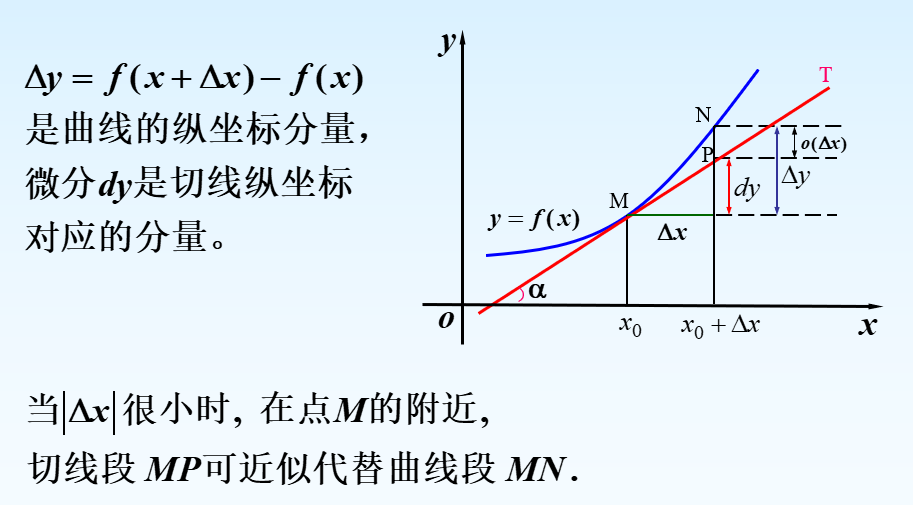
Peano余项的Taylor定理


麦克劳林公式
x0=0处展开的Taylor公式
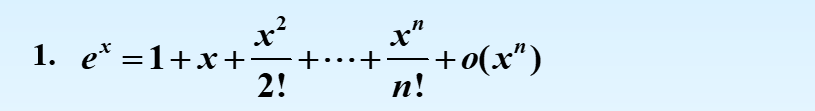
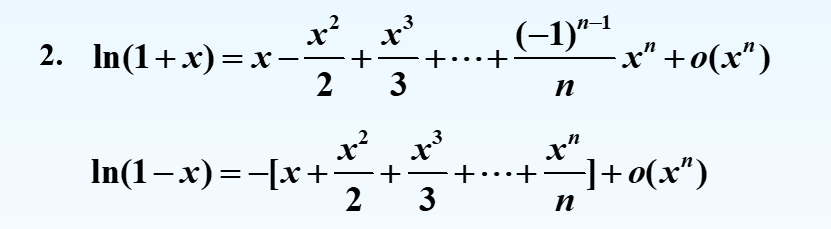
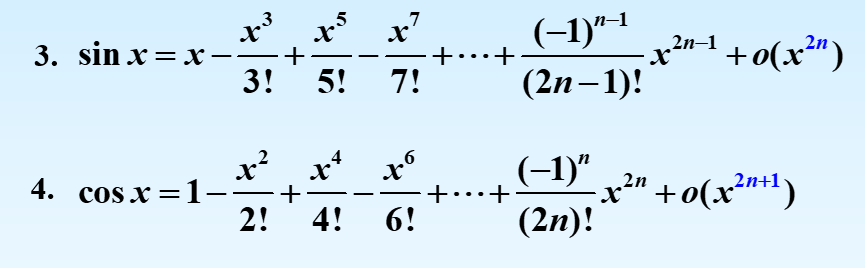
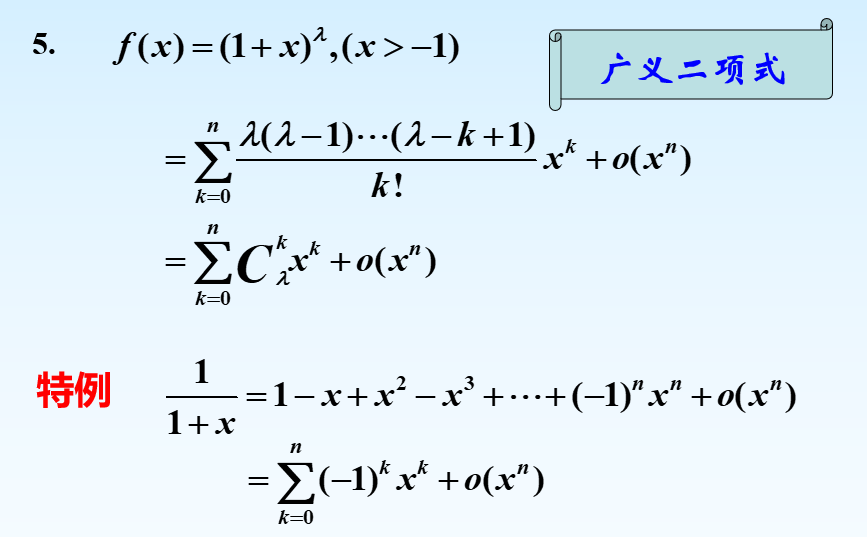
Lagrange余项的Taylor定理


偏导数
定义


链式法则

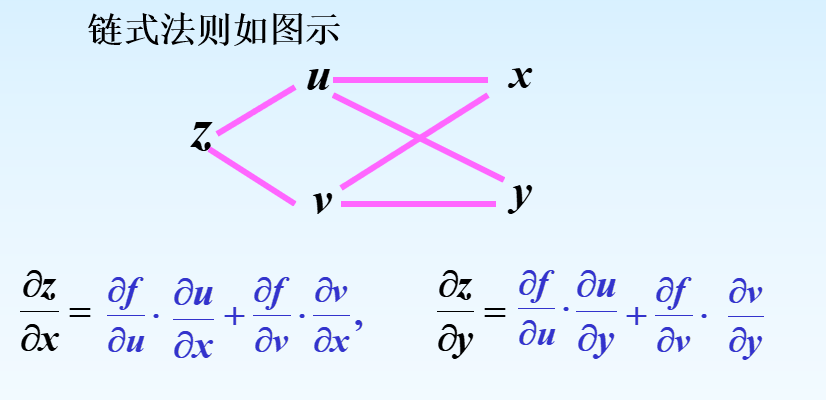
高阶偏导数

方向导数 梯度
方向导数



梯度

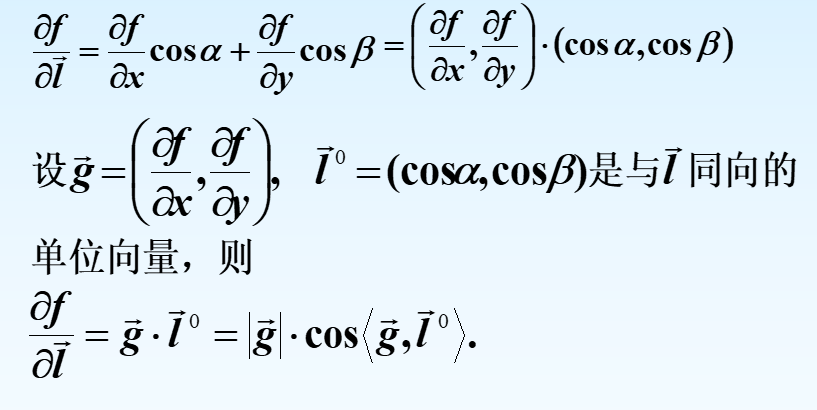



场论
数量场 向量场

梯度 $grad$ / $\nabla$


Nabla算子 $\nabla$

散度场 $divf$ / $\nabla \cdot f$
定义

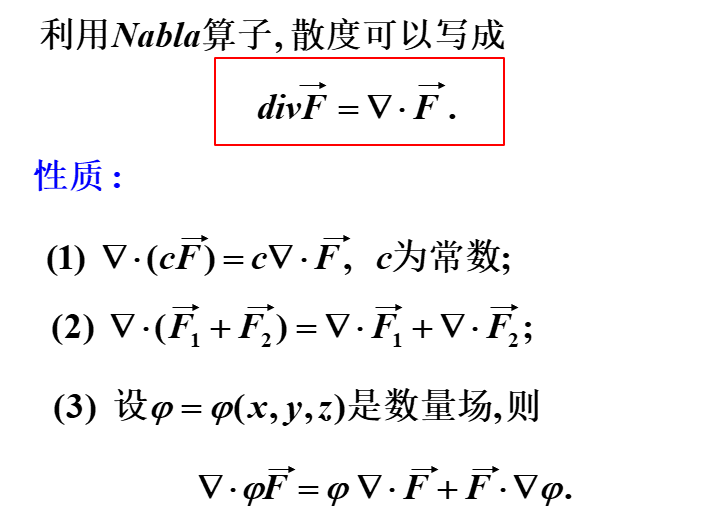
物理意义


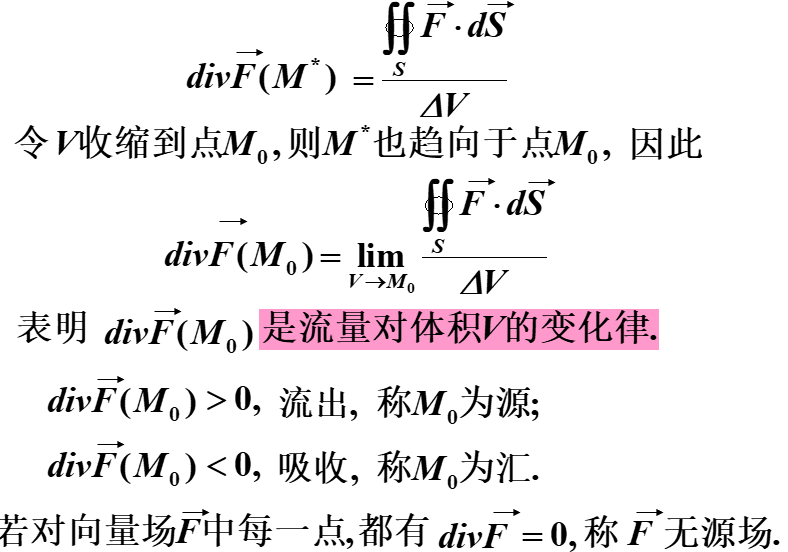
Laplace算子 $\Delta/\nabla^2$
拉普拉斯算子(Laplace Operator)是$n$维欧几里得空间中的一个二阶微分算子,定义为梯度$\nabla f$的散度$\nabla \cdot$。即$\Delta f = \nabla^2 f= \nabla \cdot \nabla f = div(gradf)$,假设f是n维函数,$\Delta f = \Sigma_i \frac{\partial^2 f}{\partial^2 x_i^2}$。

旋度场 $rotf$ / $\nabla \times f$
定义


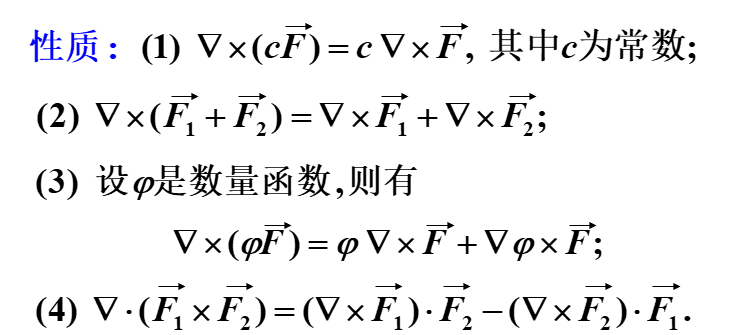
物理意义



有势场 无旋场 保守场



欧拉公式
\[e^{ix} = cosx + i \cdot sinx\] \[e^{-ix} = cosx - i \cdot sinx\]
傅里叶级数
三角函数系


傅里叶级数($T=2\pi$)

傅里叶系数
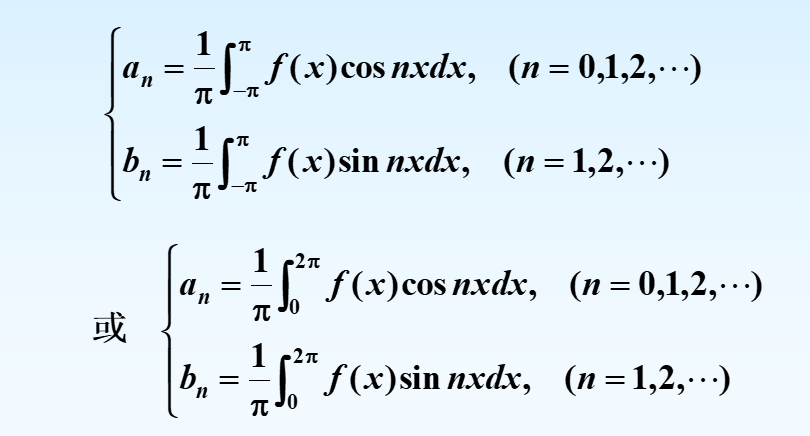
意义

以2L为周期的傅里叶级数

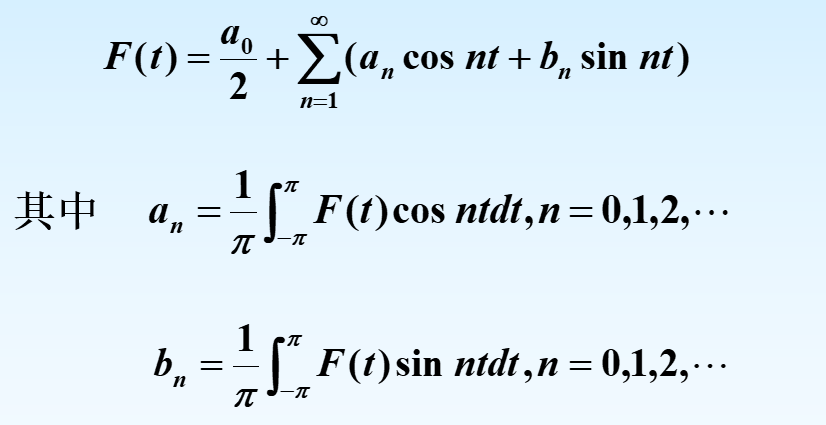

傅里叶变换
傅里叶积分
以2T为周期的傅里叶展开:
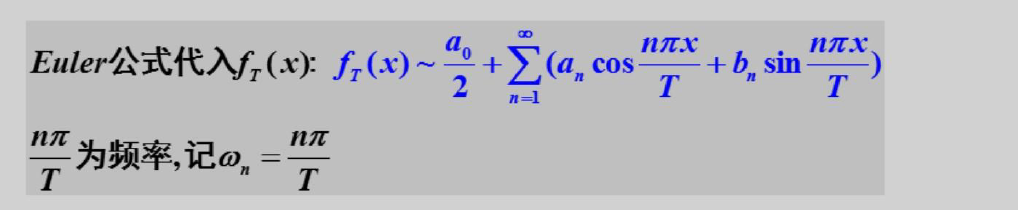
可以化简成
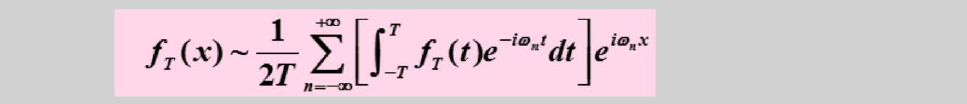

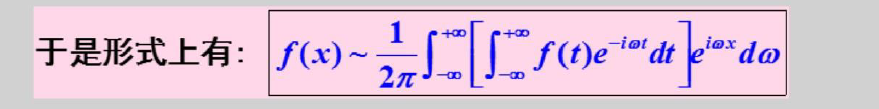
定义

傅里叶变换
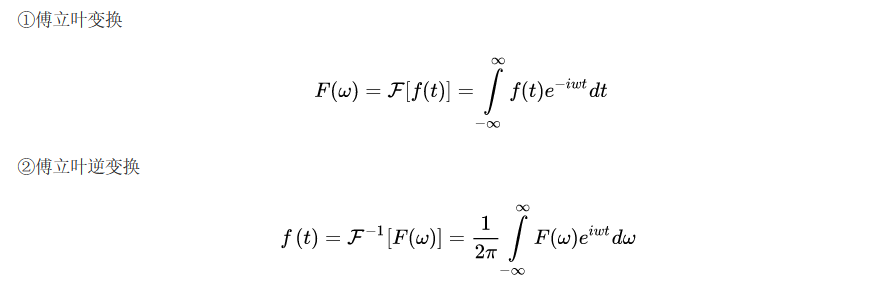

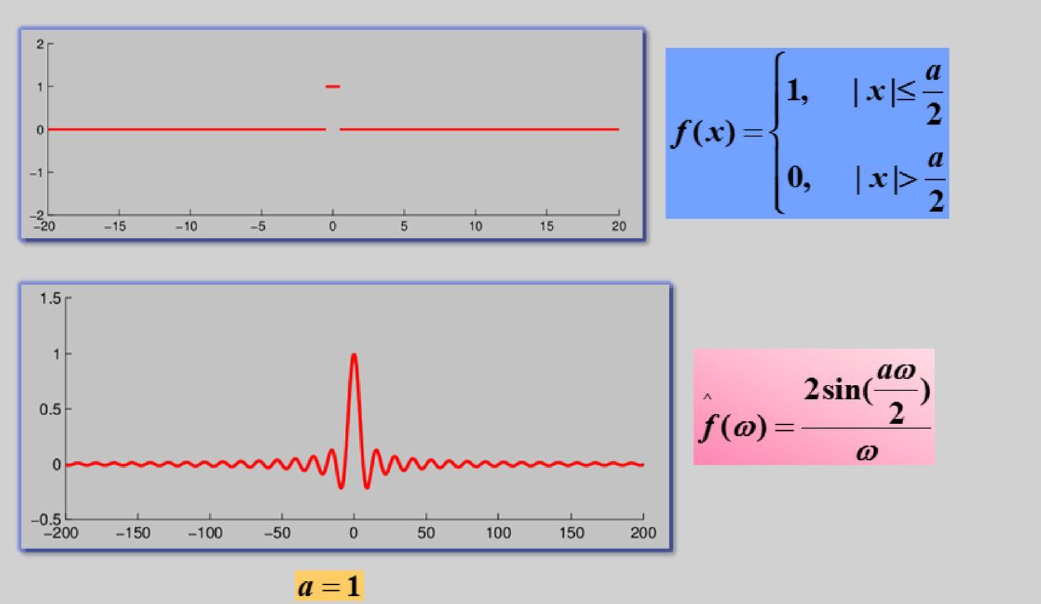
傅里叶逆变换

傅里叶积分的三角形式


傅里叶变换的性质



卷积和傅里叶变换

帕塞瓦尔等式

离散傅里叶变换




快速傅里叶变换 FTT
拉格朗日乘子法



【求出驻点之后,判断驻点是不是极值点即可】
随机过程





马尔科夫过程
马尔可夫过程是一类特殊的随机过程,马尔可夫链是离散状态的马尔可夫过程。
马尔科夫链的定义

转移概率


齐次马尔科夫链

转移概率矩阵



切普曼-柯尔莫哥洛夫方程
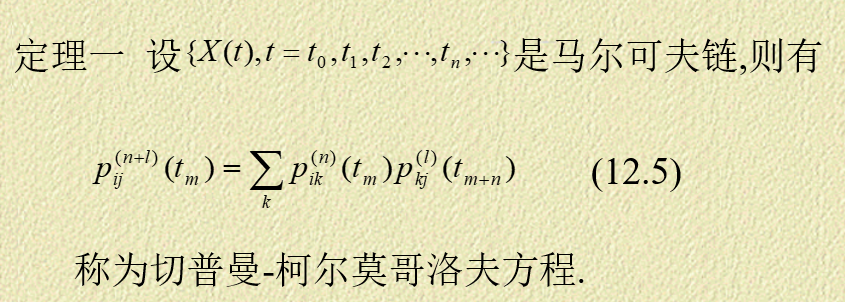

初始分布


瞬时概率


平稳分布


【就是任意时刻的分布都是相同的】
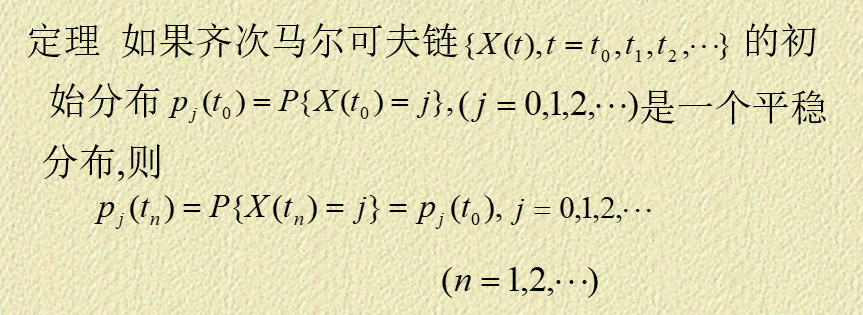
例子:
状态转移概率矩阵:
P = [[ 0.65 0.28 0.07] [ 0.15 0.67 0.18] [ 0.12 0.36 0.52]]
初始分布:(0.72,0.19,0.09)
状态转移:(0.72,0.19,0.09)* P = (0.5073, 0.3613, 0.1314) … 最后趋于稳定 (0.287 0.489 0.225)
初始分布:(0.51,0.34,0.15)
状态转移:(0.51,0.34,0.15)* P = (0.4005, 0.4246, 0.1749) … 最后趋于稳定 (0.287 0.489 0.225)
….
收敛的行为和初始概率分布无关,而是由概率转移矩阵P决定的。
计算n步转移概率矩阵\(P^{(n)} = P^n\):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0 [[ 0.65 0.28 0.07]
[ 0.15 0.67 0.18]
[ 0.12 0.36 0.52]]
1 [ [ 0.4729 0.3948 0.1323]
[ 0.2196 0.5557 0.2247]
[ 0.1944 0.462 0.3436]]
...
18 [[ 0.28650397 0.48852059 0.22497545]
[ 0.28650052 0.48852191 0.22497757]
[ 0.28649994 0.48852213 0.22497793]]
19 [[ 0.28650272 0.48852106 0.22497622]
[ 0.28650093 0.48852175 0.22497732]
[ 0.28650063 0.48852187 0.2249775 ]]
...
发现当n足够大的时候, 矩阵P收敛且每一行都稳定收敛到平稳分布(0.287 0.489 0.225)。


细致平稳条件

满足细致平稳条件的概率分布\(\pi(x)\)是状态转移矩阵P的平稳分布。
转载请标明如下内容:
本文作者:姜佳伟
本文链接:https://aptx1231.github.io/2021/02/08/%E5%9F%BA%E7%A1%80%E6%95%B0%E5%AD%A6/
Github:aptx1231

