MCMC
马尔科夫链蒙特卡罗(Markov Chain Monte Carlo,简称MCMC)是一种随机采样方法,在机器学习、深度学习等领域有广泛的应用。
蒙特卡罗方法
蒙特卡罗方法是一种随机模拟的方法,在20世纪40年代,在冯·诺伊曼,斯塔尼斯拉夫·乌拉姆和尼古拉斯·梅特罗波利斯在洛斯阿拉莫斯国家实验室为核武器计划工作时,发明了蒙特卡罗方法。
蒙特卡罗方法最初的应用是求数值积分。对定积分$\int_b^af(x)dx$,如果$f(x)$的原函数难以求解,可以使用蒙特卡洛方法求解其数值解。假设x在[a,b]的概率密度函数为$p(x)$,那么上述定积分可以转化为$\int_a^b f(x)dx = \int_a^b \frac{f(x)}{p(x)}p(x)dx \approx \frac{1}{n}\sum\limits_{i=0}^{n-1}\frac{f(x_i)}{p(x_i)}$,其中$x_i$为服从$p(x)$的样本。
给定一个概率密度函数$p(x)$,如何生成服从该概率密度函数$p(x)$的样本呢,这也是蒙特卡洛方法解决的主要问题。
简单采样方式
给定概率密度函数(probability density function, PDF)$p(x)$可以求出其累计分布函数(cumulative distribution function ,CDF)$F(x)$,$F(x)$是一个值域为[0,1]的函数。
利用线性同余发生器可以很容易的得到服从均匀分布$U(0,1)$的采样样本$y_1,y_2….y_n$,那么就可以得到$F^{-1}(y_1),F^{-1}(y_2)…F^{-1}(y_n)$即是服从$p(x)$的样本。但是并不是所有的$p(x)$都可以很容易的求得$F(x)$。
拒绝-接受采样
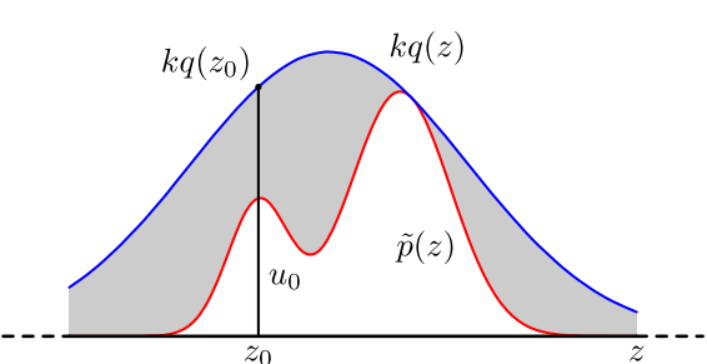
设$p(z)$是难以采样的概率密度函数,可以使用方便采样的常见密度函数$q(z)$(称为 proposal distribution)和一个常数$k$,使得$kq(z)$图像总是在$p(x)$的上方。
首先对$q(z)$采样一个样本$z_0$,然后采样$u_0$服从$U(0, kq(z_0))$,假如$u_0 \leq p(z_0)$,则接收样本$z_0$,否则拒绝样本$z_0$,重复以上过程可得到n个接受的样本$z_0,z_1,…z_{n-1}$,其服从$p(x)$。其中,$\alpha = p(z_0)/k q(z_0)$,成为接受率,显然$0 \leq \alpha \leq 1$。
马尔科夫链
马尔可夫过程是一类特殊的随机过程,马尔可夫链是离散状态的马尔可夫过程,其最初是由俄国数学家马尔可夫在1896年提出。马尔可夫链的应用领域涉及计算机、通信、自动控制等多个领域。
基本概念
关于马尔科夫链有如下几个概念需要介绍:
(1)马尔科夫链的定义
设随机过程$\lbrace X(t), t \in T \rbrace$的状态空间S是有限集或可数集,对任意正整数n,对于T中的任意n+1个参数$t_1<t_2…<t_n<t_{n+1}$和S中任意n+1个状态$j_1,j_2,…,j_n,j_{n+1}$,如果满足 $P\lbrace X(t_{n+1})=j_{n+1} | X(t_1)=j_1, X(t_2)=j_2, …, X(t_n)=j_n \rbrace=P\lbrace X(t_{n+1})=j_{n+1} | X(t_n)=j_n \rbrace$恒成立,则称此随机过程为马尔科夫链,这个式子称为马尔科夫性(也称无后效性)。
(2)转移概率和转移概率矩阵
设$\lbrace X(t), t = t_0,t_1,…,t_n,… \rbrace$是马尔科夫链,设状态空间$S={0,1,2,…n,…}$,则条件概率 $p_{ij}(t_m)=P\lbrace X(t_{m+1})=j|X(t_m)=i \rbrace$称为$X(t)$在$t_m$时刻由状态i转移到状态j的(一步)转移概率。
对S中任意两个状态i和j,由转移概率$p_{ij}$排序成的矩阵称为(一步)转移概率矩阵P。
(3)齐次马尔科夫链
假设转移概率$p_{ij}(t_m)$不依赖于参数$t_m$,即对$t_m \neq t_k$,满足 $p_{ij} =P\lbrace X(t_{m+1})=j|X(t_m)=i) \rbrace=P\lbrace X(t_{k+1})=j|X(t_k)=i) \rbrace$,则称马尔科夫链$X(t)$具有齐次性,为齐次马尔科夫链。
(4)瞬时概率
马尔科夫链在任何时刻$t_n$的一维概率分布$\pi_j(t_n)=P\lbrace X(t_n)=j \rbrace, j=0,1,2,…$成为绝对概率或瞬时概率。
(5)平稳分布
对于齐次马尔科夫链$\lbrace X(t), t \in T \rbrace$,如果存在概率分布$\pi_j,j=0,1,2…$满足$\pi_j=\sum_{i=0}^{+∞}\pi_ip_{ij},j=0,1,2…$则称概率分布$\pi_j,j=0,1,2…$为平稳分布,且$\lbrace X(t), t \in T \rbrace$具有平稳性,是平稳齐次马尔科夫链。
用向量表示的话则为$\pi = [\pi_1,\pi_2,…,\pi_j,…]\ \ \sum\limits_{i=0}^{\infty}\pi_i = 1, \ \ \pi P=\pi $,其中$\pi$称为马尔科夫链的平稳分布。
(6)细致平稳条件
如果非周期马尔科夫链的状态转移矩阵P和概率分布$\pi(x)$对于所有的i,j满足$\pi(i)P(i,j) = \pi(j)P(j,i)$,则称该马尔科夫链满足细致平稳条件,可证满足细致平稳条件的概率分布$\pi(x)$是状态转移矩阵P的平稳分布。
基于马尔科夫链的采样
如果我们得到了某个平稳分布的马尔科夫链的状态转移矩阵,就可以很容易采用出这个平稳分布的样本集。
假设任意初始的概率分布是$π_0(x)$, 经过第一轮马尔科夫链状态转移后的概率分布是$π_1(x)$….经过n轮后马尔科夫链收敛到达平稳分布$π(x)$,即:$\pi_n(x) = \pi_{n+1}(x) = \pi_{n+2}(x) =… = \pi(x)$且$\pi_i(x) = \pi_{i-1}(x)P = \pi_{i-2}(x)P^2 = \pi_{0}(x)P^i$。
基于马尔科夫链的采样过程如下:首先对初始的概率分布$π_0(x)$采样得到$x_0$,基于马尔科夫链的转移概率即条件概率分布 $P(x|x_0)$可以采样到值$x_1$, 基于条件概率分布 $P(x|x_1)$可以采样到值$x_2$,循环进行下去,当状态转移进行到一定的次数时得到的样本集$(x_n,x_{n+1},x_{n+2},…)$即是符合平稳分布$\pi(x)$的样本集。
MCMC采样
一般情况下目标平稳分布$\pi(x)$和马尔科夫链状态转移矩阵Q不满足细致平稳条件,即$\pi(i)Q(i,j) \neq \pi(j)Q(j,i)$。可以引入一个$α(i,j)$可使上式成立,即$\pi(i)Q(i,j)\alpha(i,j) = \pi(j)Q(j,i)\alpha(j,i)$。
显然,一个简单的$α(i,j)$的定义为$\alpha(i,j) = \pi(j)Q(j,i)$和$\alpha(j,i) = \pi(i)Q(i,j)$。
此时就可以得到目标平稳分布$\pi(x)$所对应的马尔科夫链状态转移矩阵P,即$P(i,j) = Q(i,j)\alpha(i,j)$。一般称$α(i,j)$为接受率,其取值在[0,1]之间。得到状态转移矩阵P之后,即可以通过如下过程进行采样了:
从任意简单概率分布采样得到$x_0$,对任意的$t$,从条件概率分布 $Q(x|x_t)$中采样得到样本$x_\star$,从均匀分布$U(0,1)$采样得到u,如果$u<α(x_t,x_\star)=\pi(x_\star) Q(x_\star,x_t)$,则接受转移$x_t \to x_\star$,即$x_{t+1}= x_\star$,否则不接受转移,即$x_{t+1}= x_{t}$。假设转移到平稳状态需要$n_1$次,需要样本数为$n_2$,则样本集即$(x_{n_1}, x_{n_1+1},…, x_{n_1+n_2-1})$为我们需要的平稳分布$π(x)$所对应的样本集。
由于接受率$α(x_t,x_\star)$一般较小,这就导致了大部分的采样值会被拒绝转移,采样效率很低。常用的改进的MCMC采样方法有Metropolis-Hastings采样(M-H采样)和Gibbs采样。
Metropolis-Hastings采样
M-H采样的主要改进思想是设置$\alpha(i,j) = min\lbrace \frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1 \rbrace$,其采样过程如下:
从任意简单概率分布采样得到$x_0$,对任意的$t$,从条件概率分布 $Q(x|x_t)$中采样得到样本$x_\star$,从均匀分布$U(0,1)$采样得到u,如果$u<α(x_t,x_\star)=min\lbrace \frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1 \rbrace$,则接受转移$x_t \to x_\star$,即$x_{t+1}= x_\star$,否则不接受转移,即$x_{t+1}= x_{t}$。假设转移到平稳状态需要$n_1$次,需要样本数为$n_2$,则样本集即$(x_{n_1}, x_{n_1+1},…, x_{n_1+n_2-1})$为我们需要的平稳分布$π(x)$所对应的样本集。
Gibbs采样
对于高维的数据分布,Metropolis-Hastings采样算法的效率较低,Gibbs采样是对M-H算法的改进。
以二维情况为例,设概率分布为$p(x,y)$,平面上两个点$A(x_1,y_1),B(x_1,y_2)$的x坐标相同,根据条件概率公式可以得到: $p(x_1,y_1)p(y_2|x_1)=p(x_1)p(y_1|x_1)p(y_2|x_1)$和$p(x_1,y_2)p(y_1|x_1)=p(x_1)p(y_2|x_1)p(y_1|x_1)$。
所以可以得到 $p(x_1,y_1)p(y_2|x_1)=p(x_1,y_2)p(y_1|x_1)$, 即$p(A)p(y_2|x_1)=p(B)p(y_1|x_1)$。
根据上式可以得到,在$x=x_1$直线上的任意两点之间,使用 $p(y|x_1)$做两点之间的转移概率,那么任意两点之间的转移满足细致平稳条件,也就是可以得到一个平稳分布$p(x,y)$。$y=y_1$时同理。
因此二维Gibbs采样过程为:
首先从任意简单概率分布采样得到$X_0=x_0,Y_0=y_0$,
之后对任意的t按照规则 $y_{t+1} \sim p(y|x_t) $和 $x_{t+1} \sim p(x|y_{t+1})$循环采样,即可得到目标样本集,且其服从平稳分布$p(x,y)$。
推广到n维的情况时,Gibbs采样过程如下:
首先从任意简单概率分布采样得到$\lbrace x_i, i=1,…,n \rbrace$。
之后对任意的$t$,按照如下方式进行循环采样,即可得到目标样本集,且其服从平稳分布$p(x_1,p_2,…,p_n)$。
\[x_1^{t+1} \sim p(x_1|x_2^{(t)}, x_3^{(t)},...,x_n^{(t)}) \\ x_2^{t+1} \sim p(x_2|x_1^{(t+1)}, x_3^{(t)},...,x_n^{(t)}) \\ …\\ x_j^{t+1} \sim p(x_j|x_1^{(t+1)},..., x_{j-1}^{(t)},...,x_n^{(t)}) \\ …\\ x_n^{t+1} \sim p(x_n|x_1^{(t+1)}, x_2^{(t+1)},...,x_{n-1}^{(t+1)}) \\\]
